Variational Autoencoders in short

Leave a Comment / Bayesian, VAE / By
Image by rawpixel.com on Freepik

Bayesian Theory

Bayesian theory provides the tools to incorporate our beliefs on how the data was generated into a model in order to interpret an observed phenomenon. These beliefs represent prior information or uncertainty.

A Bayesian problem consists of:
  • Parametric model $p(\mathbf{x}|\mathbf{z})$: joint distributions of the observations $\mathbf{x}$ given the parameters and latent variables $\mathbf{z}$. It models our beliefs on how the data was generated given $\mathbf{z}$. $\mathbf{z}$ represent the non observed variables that governs the generation of observations.
  • Prior distribution $p(\mathbf{z})$: The presumed density of the parameters $\mathbf{z}$. It models our beliefs on how the parameters look like.

Bayes' Theorem

The core theorem of this theory is, you guessed right, the Bayes’ theorem. In case of new observations (new evidence), this theorem allows us to update our beliefs. Bayes’ theorem is formulated as follows: $$p(\mathbf{z}|\mathbf{x}) = \frac{p(\mathbf{x}|\mathbf{z})p(\mathbf{z})}{p(\mathbf{x})} = \frac{p(\mathbf{x}|\mathbf{z})p(\mathbf{z})}{\int p(\mathbf{x}|\mathbf{z})p(\mathbf{z})d\mathbf{z}} $$

Variational Inference

In many Bayesian problems (for certain choices of $p(\mathbf{x}|\mathbf{z})$ and $p(\mathbf{z})$), the analytic calculation of $p(\mathbf{x})$ and accordingly that of $p(\mathbf{z}|\mathbf{x})$ might be intractable. Variational inference is one of the approaches to deal with this. In fact, variational inference approximates the posterior $p(\mathbf{z}|\mathbf{x})$ by $q(\mathbf{z}|\mathbf{x})$. The distribution $q(\mathbf{z}|\mathbf{x})$ should be chosen such that the calculations are tractable as it should be flexible to approximate the true posterior $p(\mathbf{z}|\mathbf{x})$. A common choice of $q(\mathbf{z}|\mathbf{x})$ is Gaussian distributions where the parameters are optimized to approximate $p(\mathbf{z}|\mathbf{x})$.

Variational Autoencoder

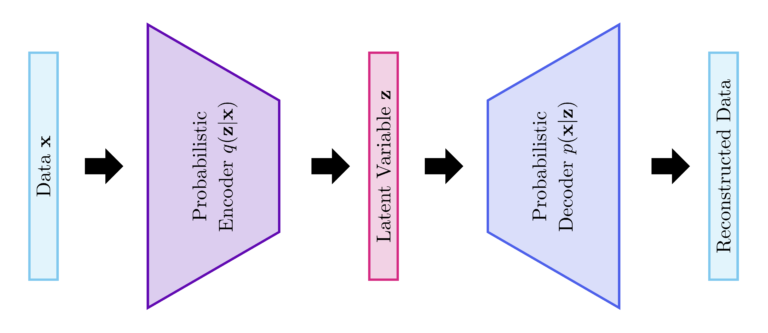
In variational autoencoders, the encoder learns $q(\mathbf{z}|\mathbf{x})$ to approximate $p(\mathbf{z}|\mathbf{x})$ while the decoder learns $p(\mathbf{x}|\mathbf{z})$. Please note that the decoder is the inverse of the encoder according to Bayes rule. The parameters of $q(\mathbf{z}|\mathbf{x})$ and $p(\mathbf{x}|\mathbf{z})$ are modeled using neural networks. In particular, the parameters of $q(\mathbf{z}|\mathbf{x})$ (resp. $p(\mathbf{x}|\mathbf{z})$) are the weights and biases of the encoder (resp. the decoder).

ELBO

The objective function optimized for the variational approximation is called the evidence lower bound and is defined as:
$$\mathcal{L}(\mathbf{x}) = \mathbb{E}_q\Big[\log\big(p(\mathbf{x}, \mathbf{z}) \big) – \log\big(q(\mathbf{z}| \mathbf{x})\big)\Big]$$

The ELBO is derived from the log likelihood as follows, \begin{eqnarray*} \log\big(p(\mathbf{x})\big) &=& \mathbb{E}_q\Big[\log\big(p(\mathbf{x})\big)\Big]\\ &=& \mathbb{E}_q\Big[\log\Big(\frac{p(\mathbf{x}, \mathbf{z})}{p(\mathbf{z}|\mathbf{x})}\Big)\Big]\\ &=& \mathbb{E}_q\Big[\log\Big(\frac{p(\mathbf{x}, \mathbf{z})q(\mathbf{z}|\mathbf{x})}{p(\mathbf{z}|\mathbf{x})q(\mathbf{z}|\mathbf{x})}\Big)\Big]\\ &=&\mathcal{L}(\mathbf{x}) + D_{KL}\big(q(\mathbf{z}|\mathbf{x})||p(\mathbf{z}|\mathbf{x})\big) \end{eqnarray*} Given the non-negativity of the Kullback-Leibler divergence, $D_{KL}\big(q(\mathbf{z}|\mathbf{x})||p(\mathbf{z}|\mathbf{x})\big)$, $\mathcal{L}(\mathbf{x})$ is a lower bound to the evidence, $\log\big(p(\mathbf{x})\big)\geq \mathcal{L}(\mathbf{x})$. Hence the name. Note that maximizing $\mathcal{L}(\mathbf{x})$ will simultaneously maximize $\log\big(p(\mathbf{x})\big)$ and minimize $D_{KL}\big(q(\mathbf{z}|\mathbf{x})||p(\mathbf{z}|\mathbf{x})\big)$.

Reparameterization trick

The gradient of the ELBO $\mathcal{L}(\mathbf{x})$ with respect to the parameters of the decoder is intractable. This can be avoided by a change of variable. In particular, $\mathbf{z}$ can be written as function of a random variable $\boldsymbol{\epsilon}$ (noise). As such, the expectation in $\mathcal{L}(\mathbf{x})$, which is w.r.t $q(\mathbf{z}|\mathbf{x})$, can be written w.r.t $p(\boldsymbol{\epsilon})$. Accordingly, the gradient and expectation become commutative. Please note that, in this case, the objective function $\mathcal{L}(\mathbf{x})$ writes,

$$\mathcal{L}(\mathbf{x}) = \mathbb{E}_q\Big[\log\big(p(\mathbf{x}, \mathbf{z}) \big) – \log\big(p(\boldsymbol{\epsilon})\big) + \log\big|\frac{\partial \mathbf{z}}{\partial \boldsymbol{\epsilon}}\big|\Big]$$

where $\log\big|\frac{\partial \mathbf{z}}{\partial \boldsymbol{\epsilon}}\big|$ denotes the log-determinant of the Jacobian matrix $\frac{\partial \mathbf{z}}{\partial \boldsymbol{\epsilon}}$. Please note that the function relating $\mathbf{z}$ and $\boldsymbol{\epsilon}$ should be chosen such that the calculation of $\log\big|\frac{\partial \mathbf{z}}{\partial \boldsymbol{\epsilon}}\big|$ is straightforward.

References

Related posts:


Leave a Comment

Your email address will not be published. Required fields are marked *